Publications
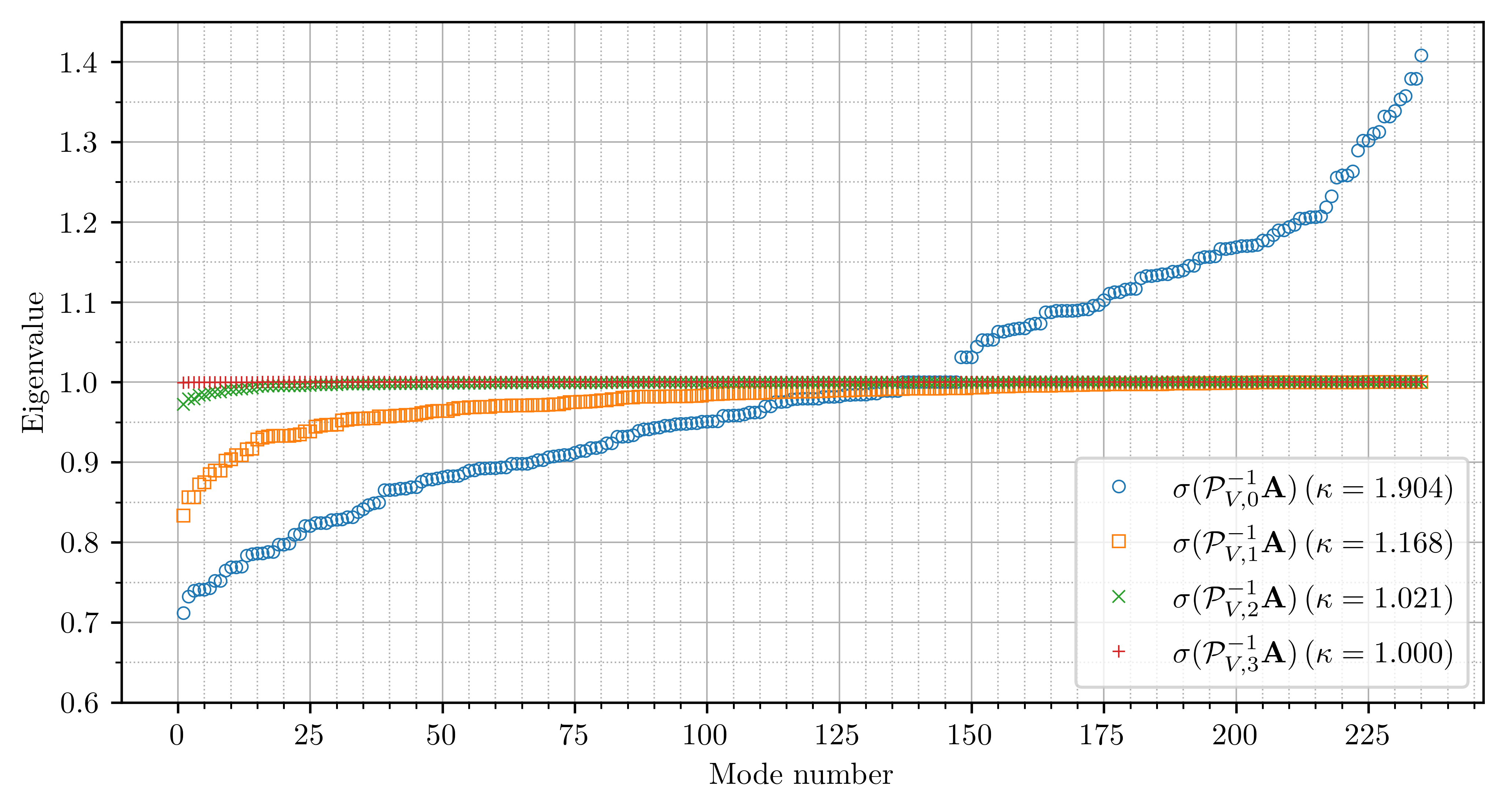
Matrix-free polynomial preconditioning of saddle point systems using the hyper-power method
M.L. Mika, M.F.P. ten Eikelder, D. Schillinger and R.R. Hiemstra
November 12, 2023;
preprint
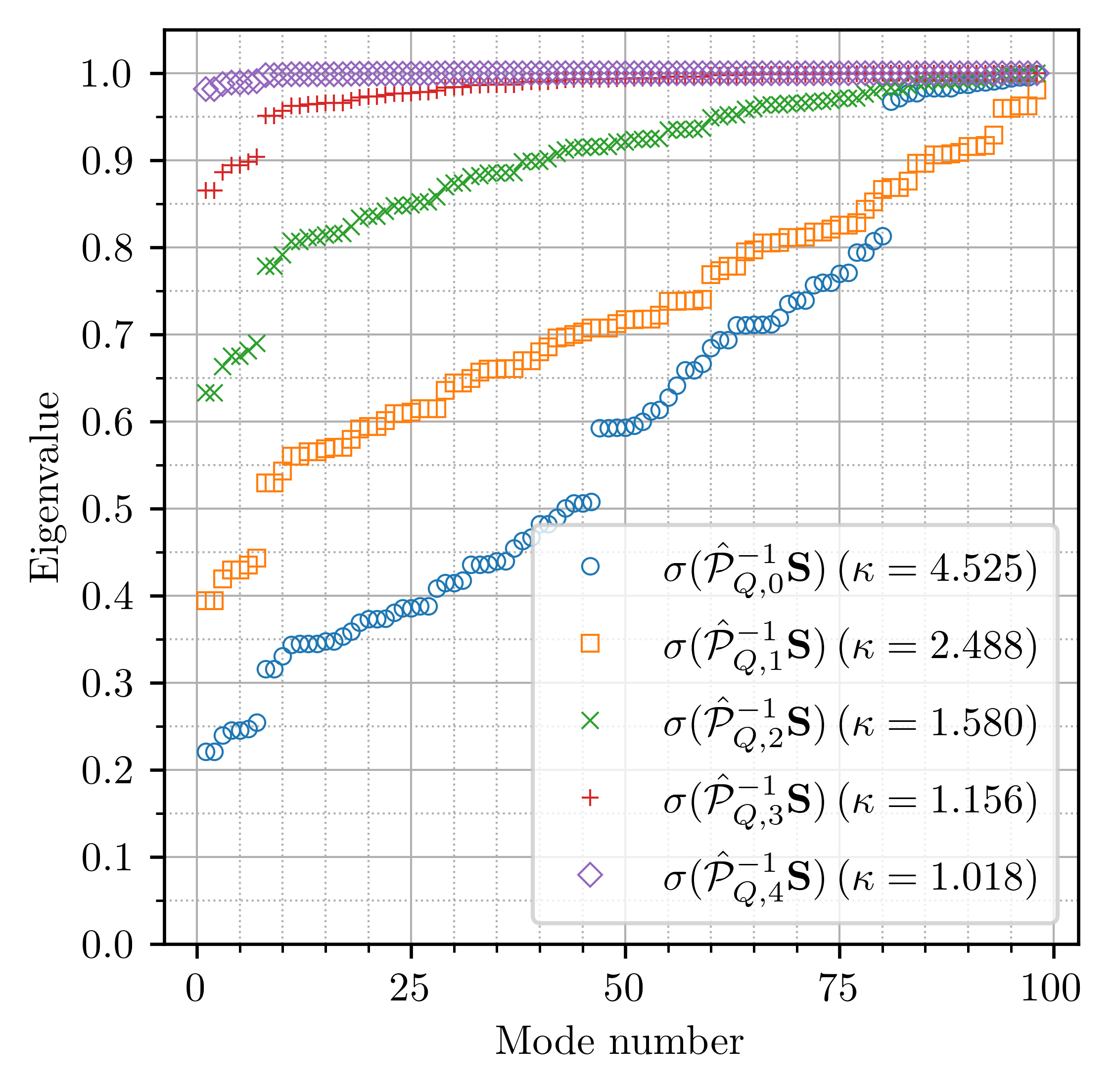
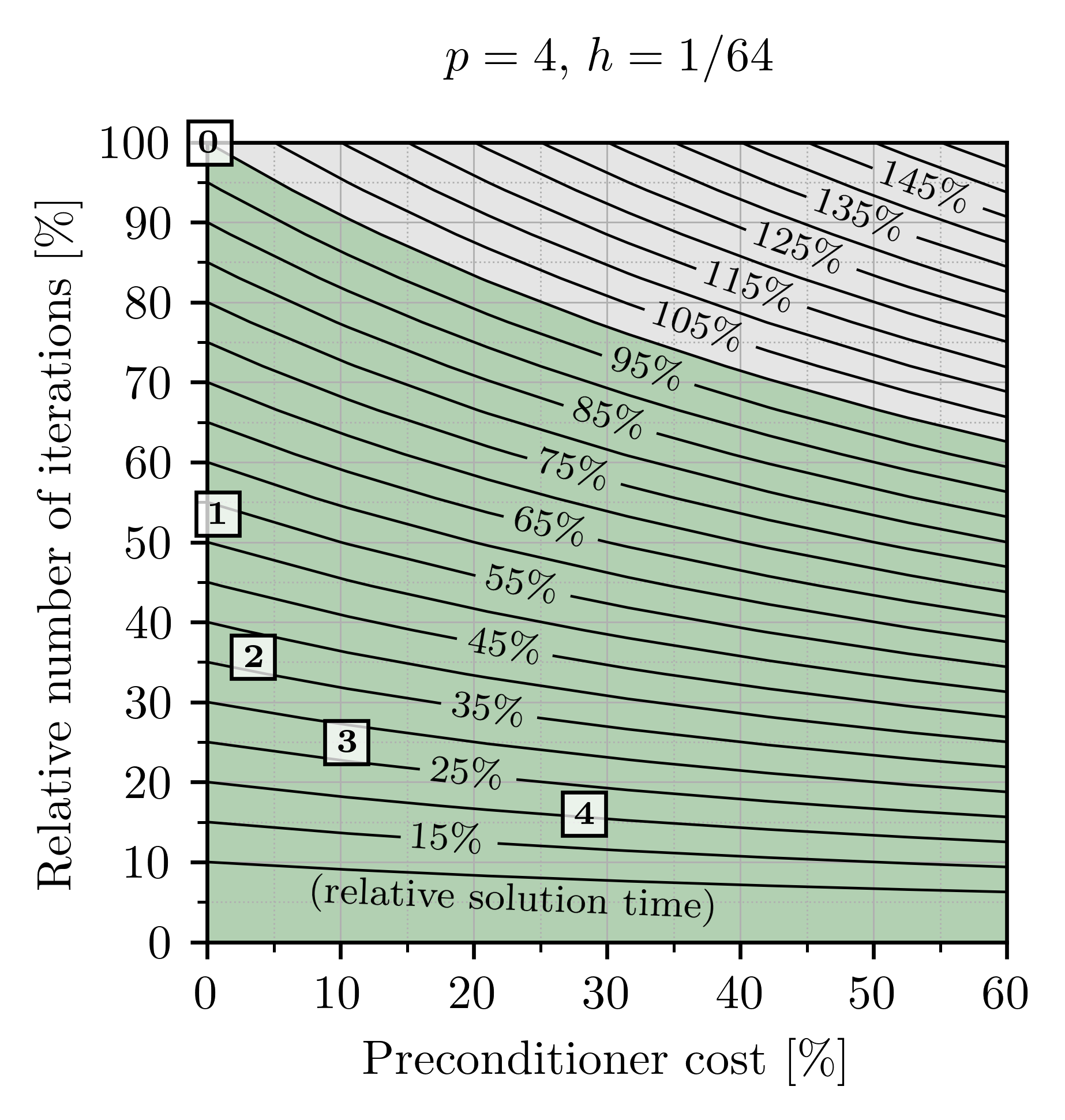
This study explores the integration of the hyper-power sequence, a method commonly employed for
approximating the Moore-Penrose inverse, to enhance the effectiveness of an existing preconditioner.
The approach is closely related to polynomial preconditioning based on Neumann series. We commence
with a state-of-the-art matrix-free preconditioner designed for the saddle point system derived
from isogeometric structure-preserving discretization of the Stokes equations. Our results
demonstrate that incorporating multiple iterations of the hyper-power method enhances the effectiveness
of the preconditioner, leading to a substantial reduction in both iteration counts and overall solution
time for simulating Stokes flow within a 3D lid-driven cavity. Through a comprehensive analysis, we
assess the stability, accuracy, and numerical cost associated with the proposed scheme.
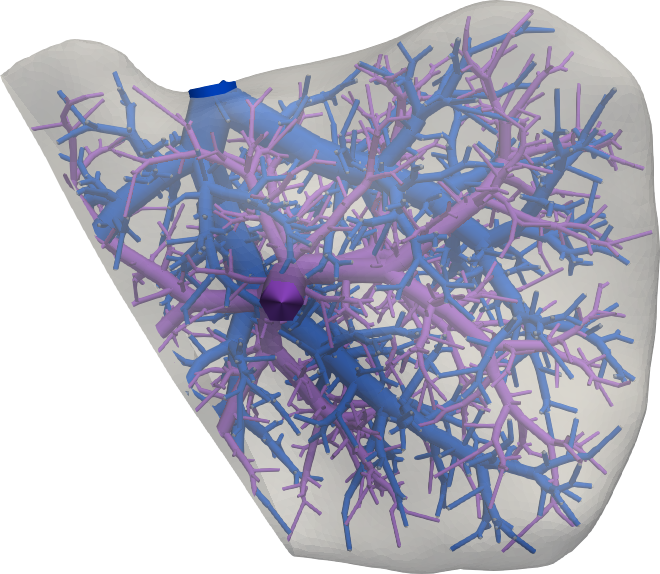
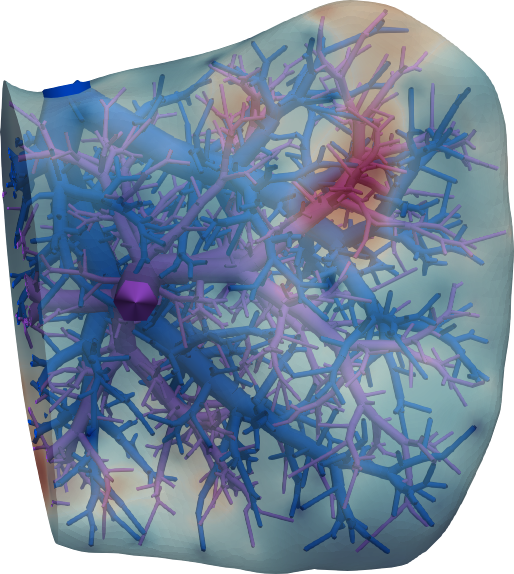
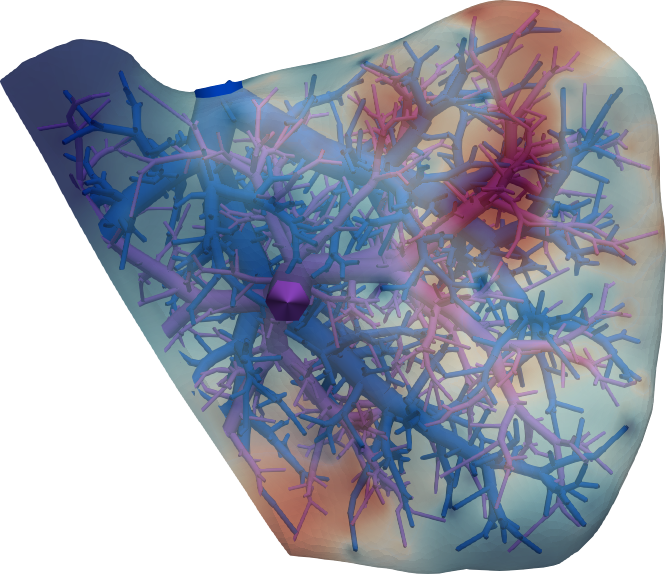
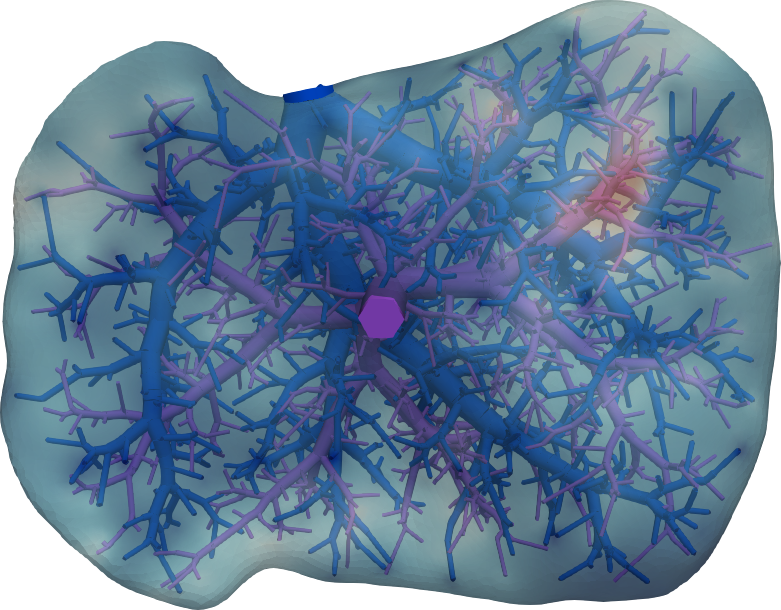
Connecting continuum poroelasticity with discrete synthetic vascular trees for modeling liver tissue
A. Ebrahem, E. Jessen, M.F.P. ten Eikelder, T. Gangwar, M. Mika and D. Schillinger
June 12, 2023;
preprint
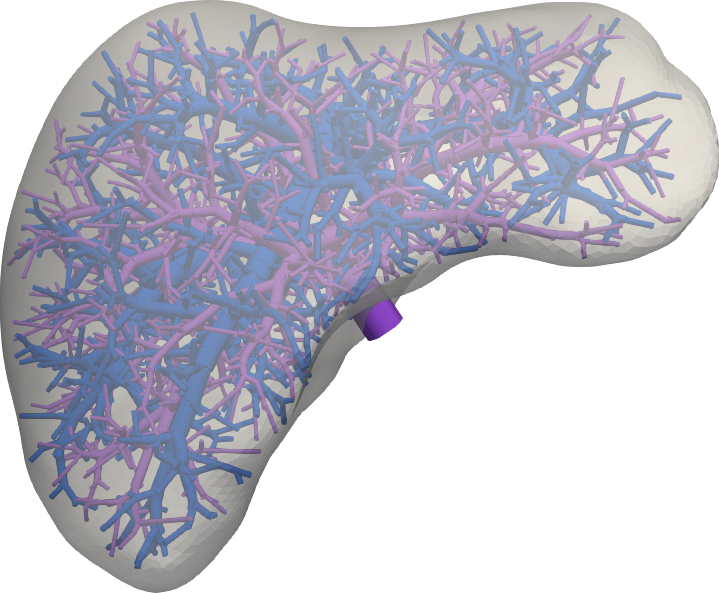
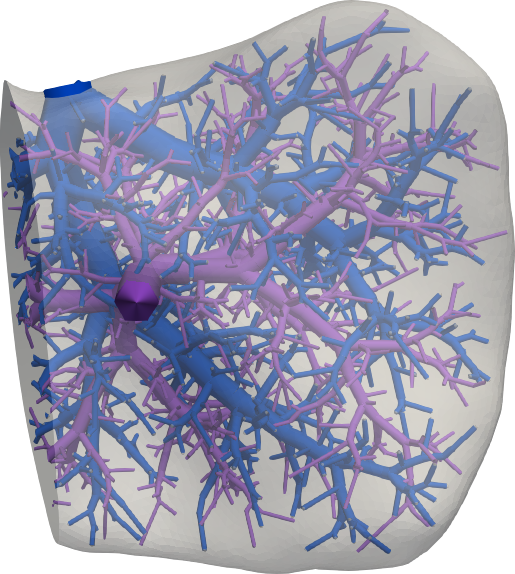
Computational simulations have the potential to assist in liver resection surgeries by facilitating
surgical planning, optimizing resection strategies, and predicting postoperative outcomes. The
modeling of liver tissue across multiple length scales constitutes a significant challenge,
primarily due to the multiphysics coupling of mechanical response and perfusion within the
complex multiscale vascularization of the organ. In this paper, we present a modeling framework
that connects continuum poroelasticity and discrete vascular tree structures to model liver tissue
across disparate levels of the perfusion hierarchy. The connection is achieved through a series of
modeling decisions, which include source terms in the pressure equation to model inflow from the
supplying tree, pressure boundary conditions to model outflow into the draining tree, and contact
conditions to model surrounding tissue. We investigate the numerical behaviour of our framework and
apply it to a patient-specific full-scale liver problem that demonstrates its potential to help assess
surgical liver resection procedures.

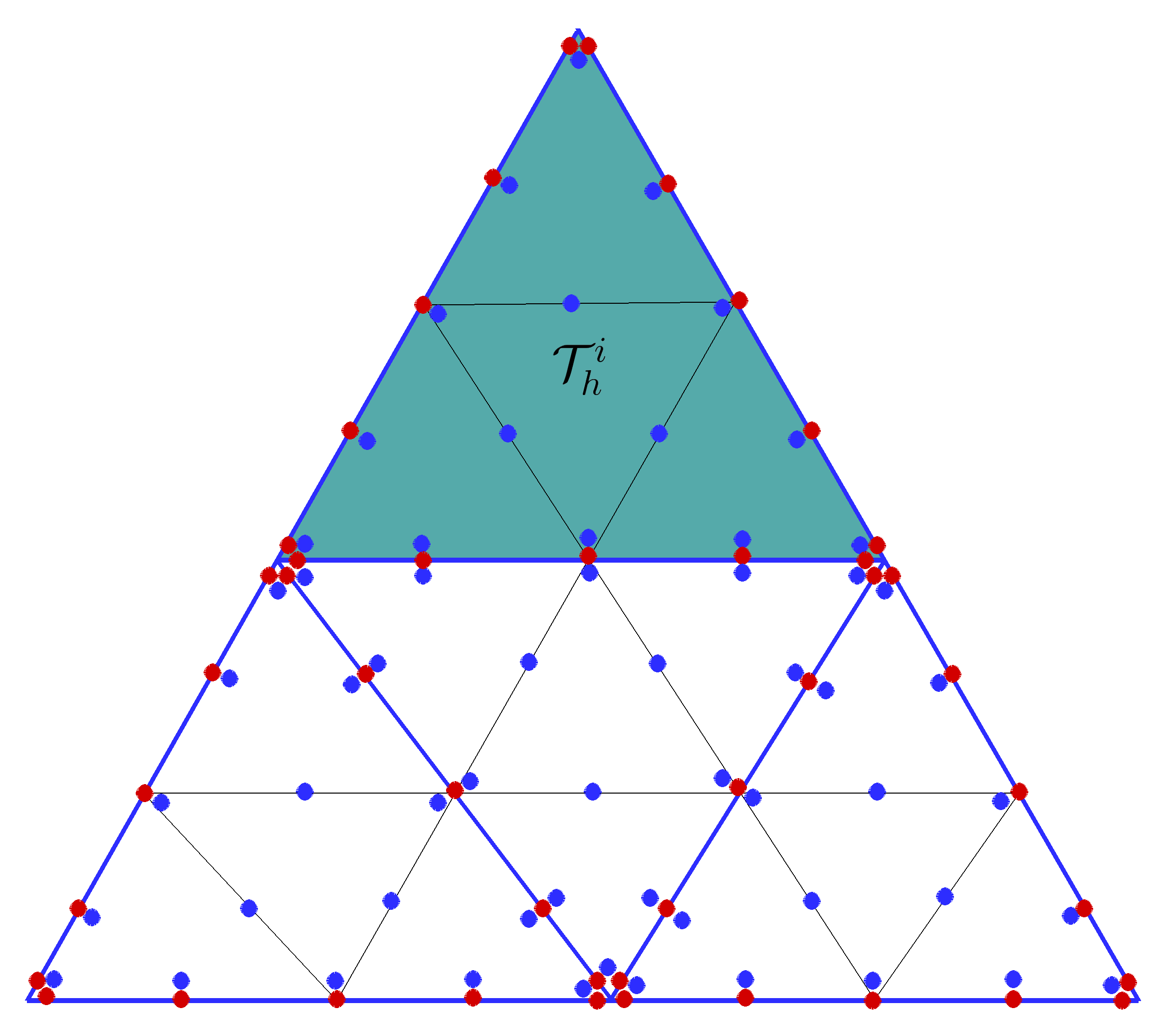
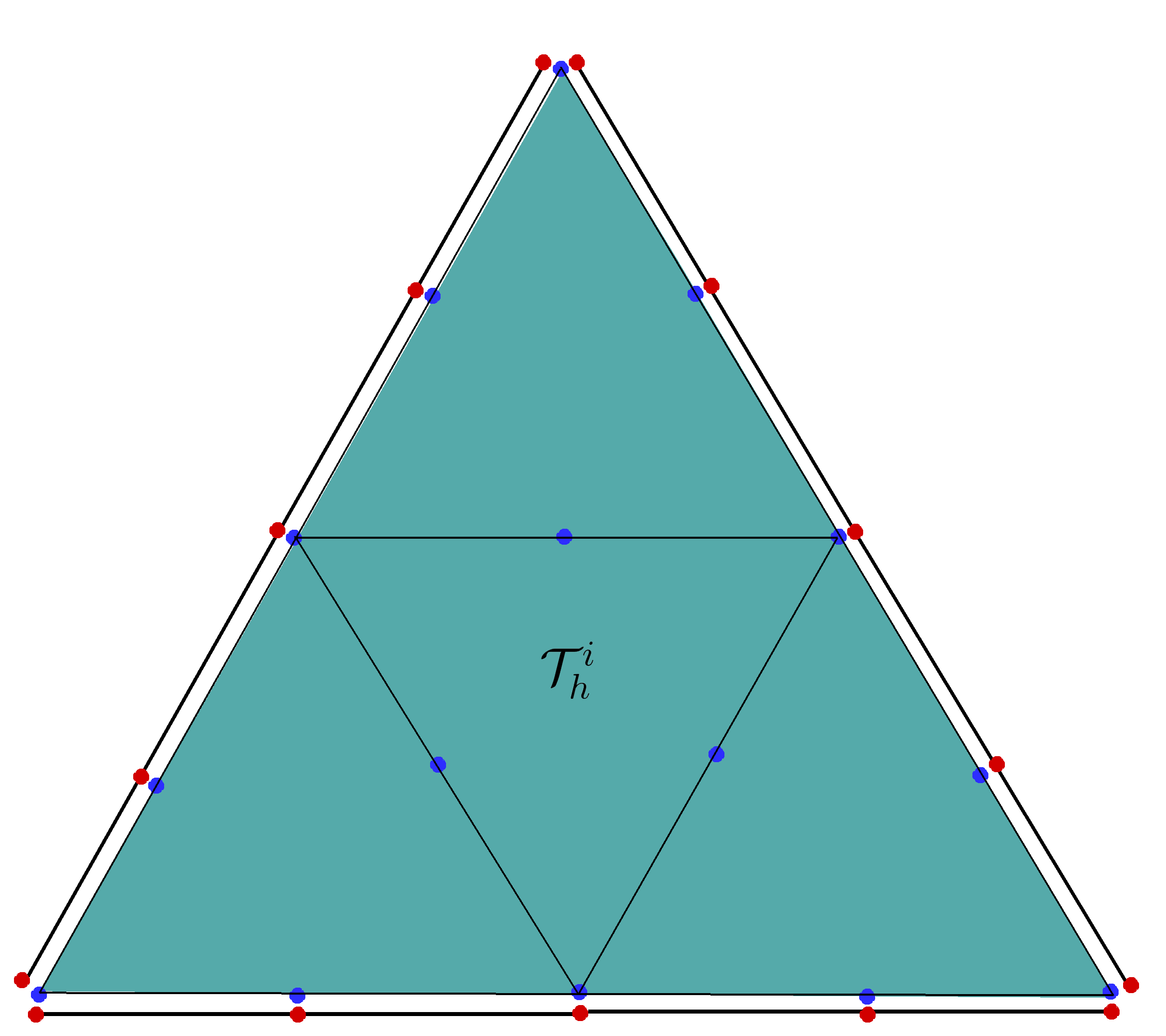
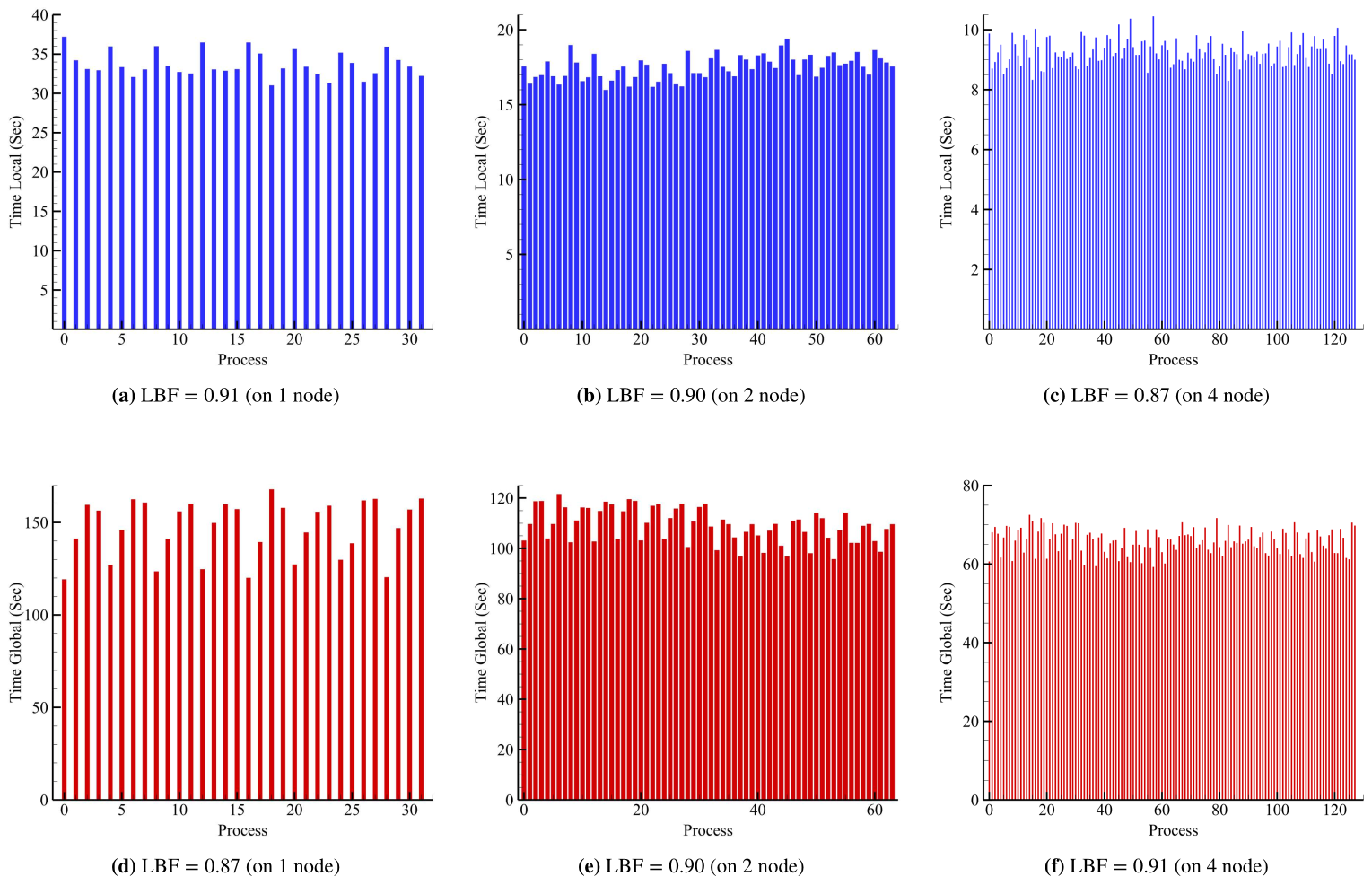
A matrix-free macro-element variant of the hybridized discontinuous Galerkin method
V. Badrkhani, R.R. Hiemstra, M.L. Mika and D. Schillinger
February 17, 2023;
International Journal for Numerical Methods in Engineering
We investigate a macro-element variant of the hybridized discontinuous Galerkin (HDG) method, using patches of
standard simplicial elements that can have non-matching interfaces. Coupled via the HDG technique, our method
enables local refinement by uniform simplicial subdivision of each macro-element. By enforcing one spatial
discretization for all macro-elements, we arrive at local problems per macro-element that are embarrassingly
parallel, yet well balanced. Therefore, our macro-element variant scales efficiently to n-node clusters and
can be tailored to available hardware by adjusting the local problem size to the capacity of a single node,
while still using moderate polynomial orders such as quadratics or cubics. Increasing the local problem size
means simultaneously decreasing, in relative terms, the global problem size, hence effectively limiting the
proliferation of degrees of freedom. The global problem is solved via a matrix-free iterative technique that
also heavily relies on macro-element local operations.
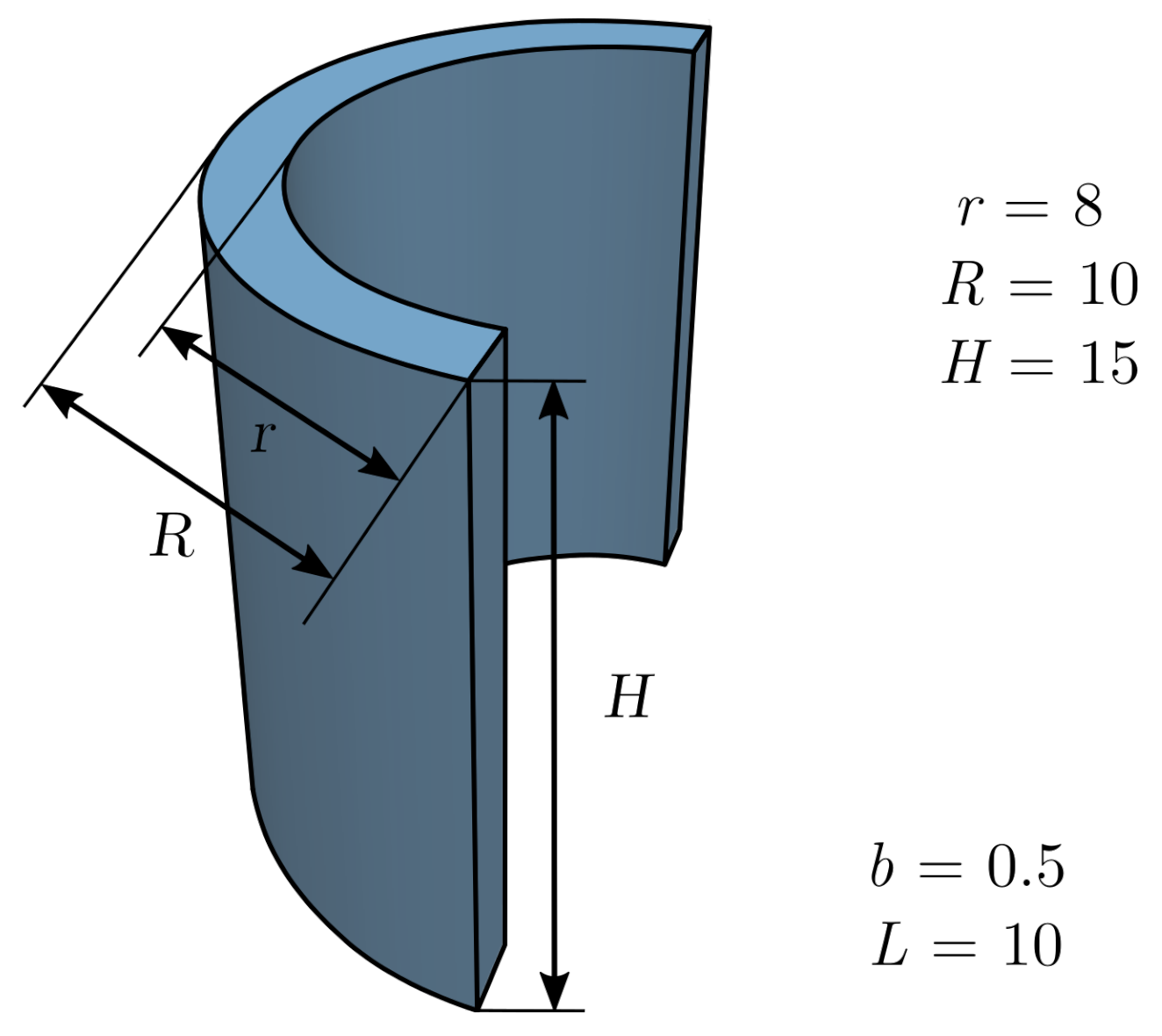
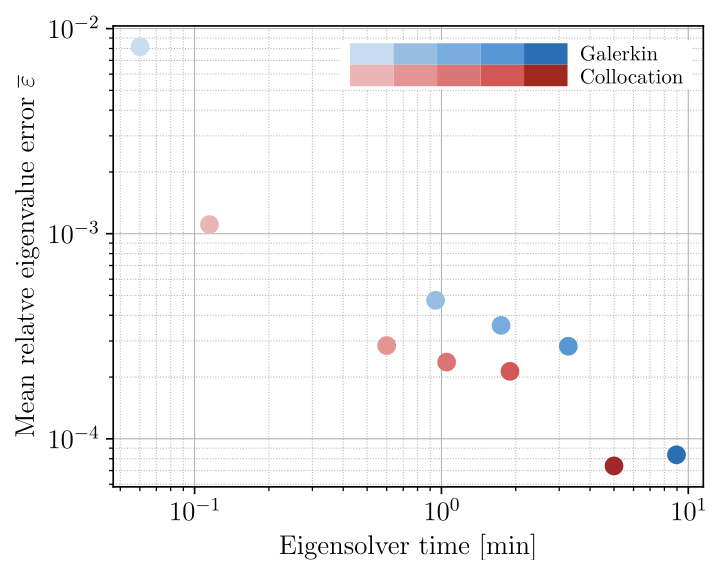
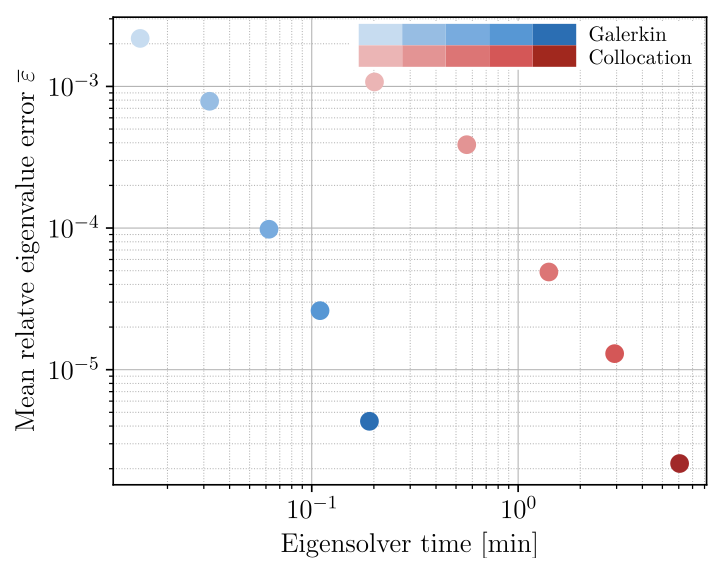
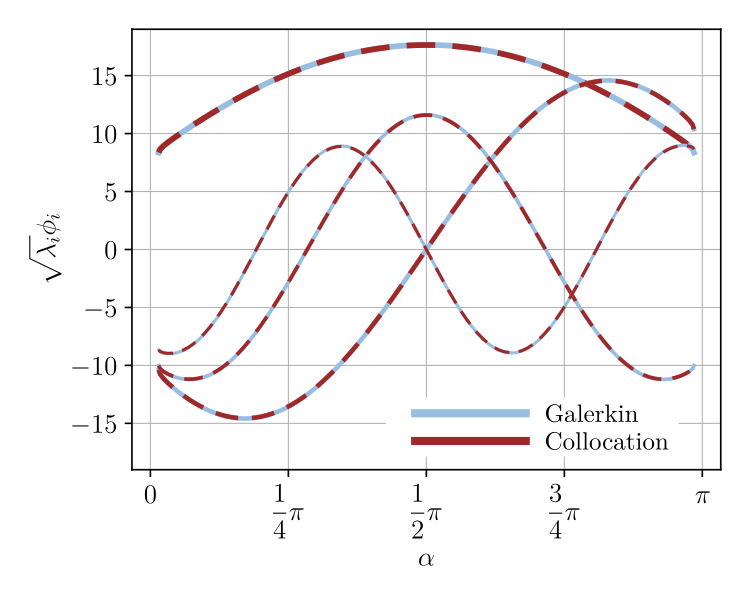
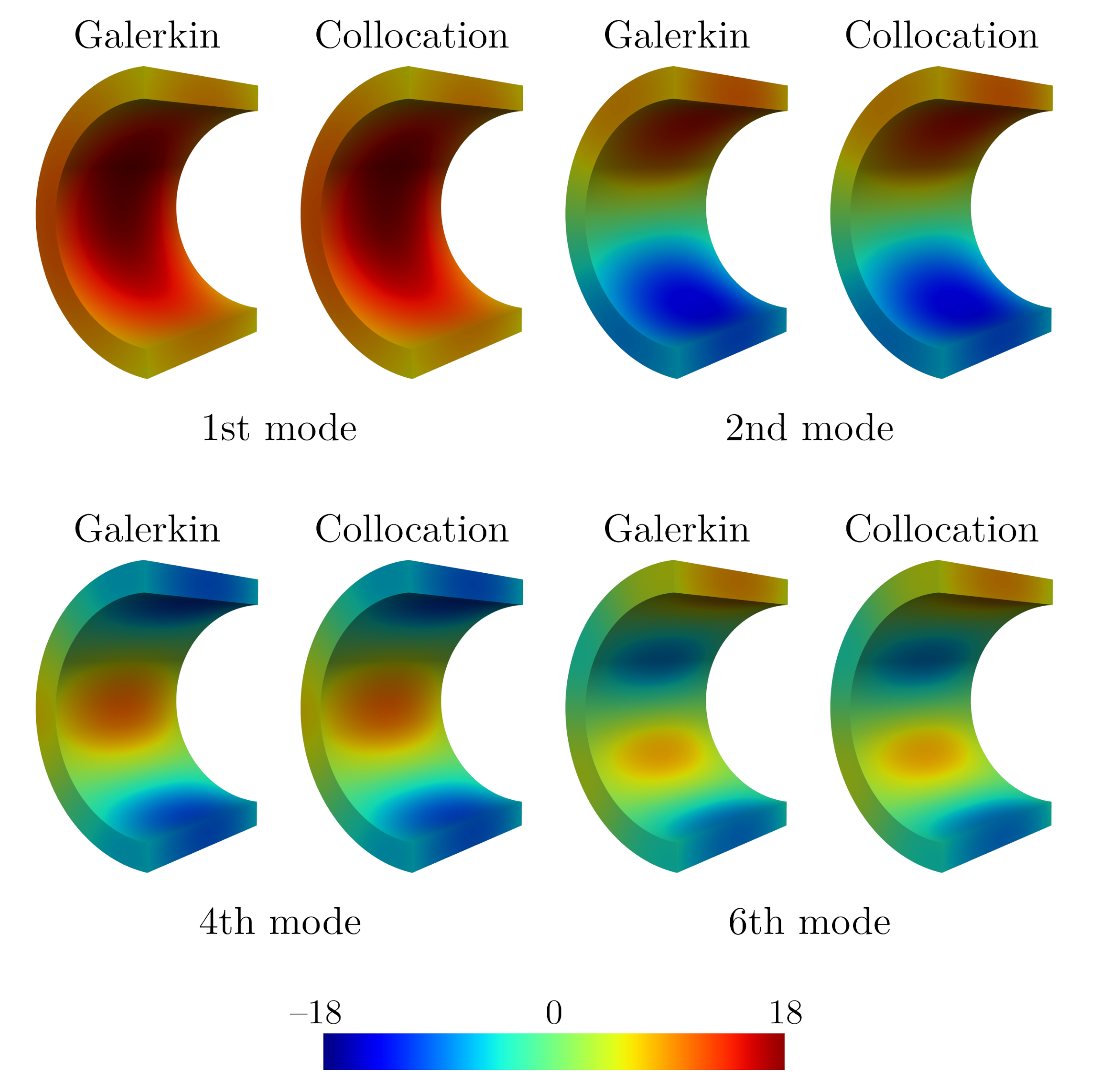
A comparison of matrix-free isogeometric Galerkin and collocation methods for Karhunen–Loève expansion
M.L. Mika, R.R. Hiemstra, T.J.R. Hughes and D. Schillinger
March 13, 2022;
Current Trends and Open Problems in Computational Mechanics
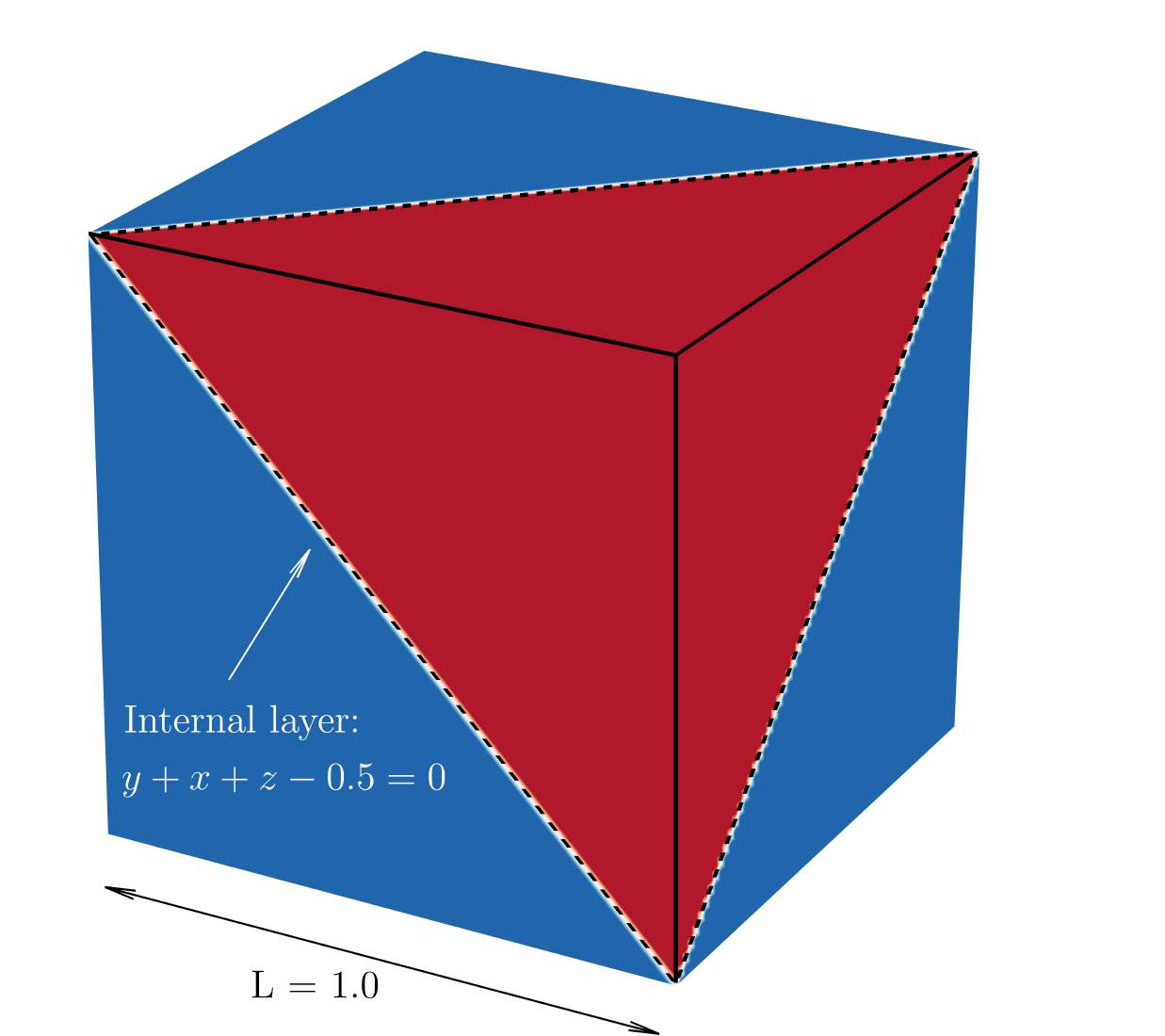
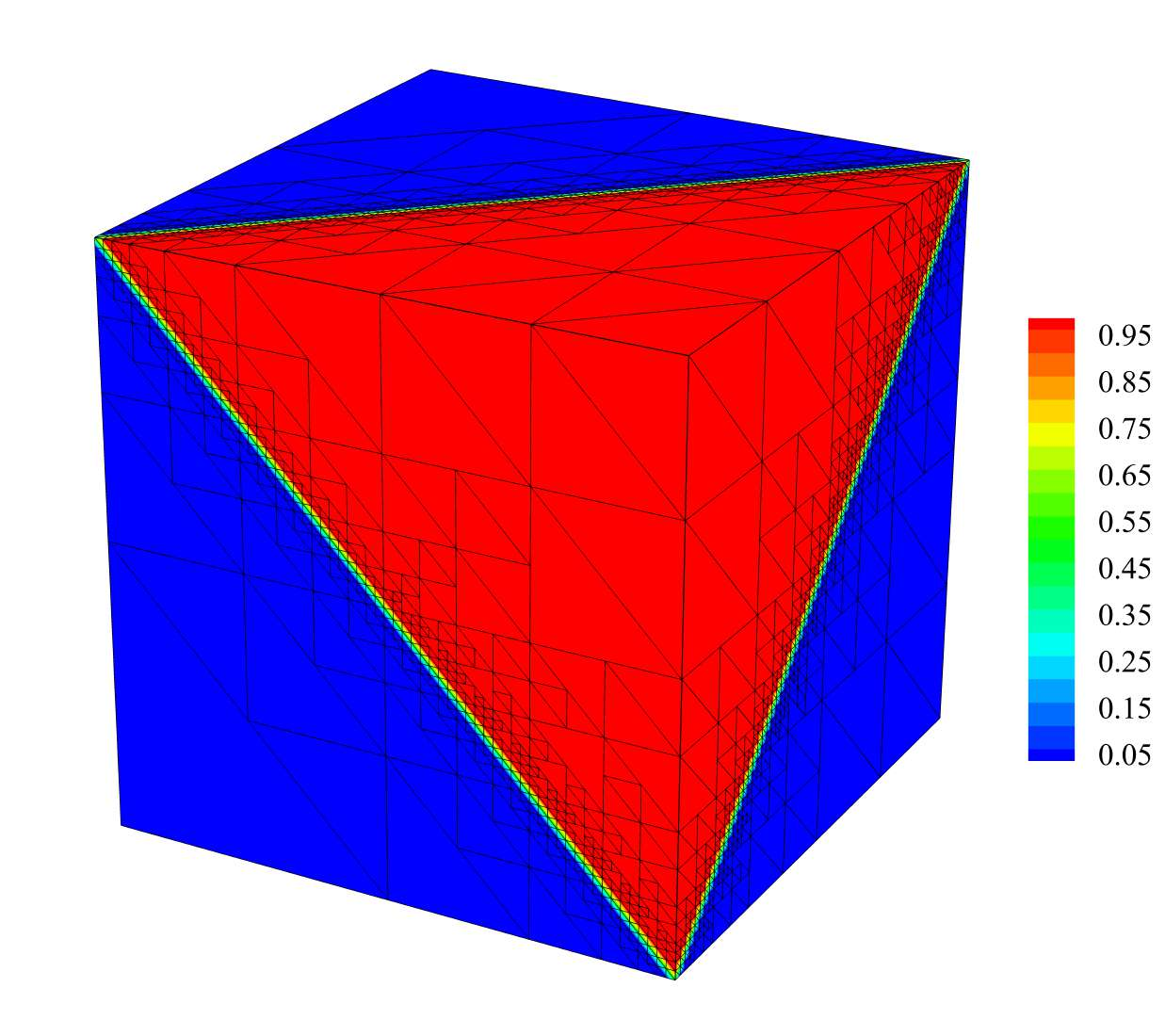
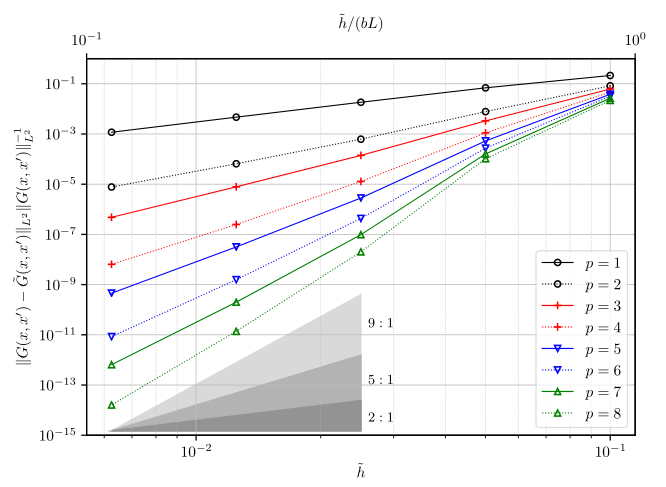
Numerical computation of the Karhunen–Loève expansion is computationally challenging in terms of both memory
requirements and computing time. We compare two state-of-the-art methods that claim to efficiently solve for the
K–L expansion: (1) the matrix-free isogeometric Galerkin method using interpolation based quadrature proposed
by the authors in [1] and (2) our new matrix-free implementation of the isogeometric collocation method proposed in [2].
Two three-dimensional benchmark problems indicate that the Galerkin method performs significantly better for smooth
covariance kernels, while the collocation method performs slightly better for rough covariance kernels.
A matrix-free isogeometric Galerkin method for Karhunen-Loève
approximation of random fields using tensor product splines, tensor
contraction and interpolation based quadrature
M.L. Mika, T.J.R. Hughes, D. Schillinger, P. Wriggers and R.R. Hiemstra
February 9, 2021;
Computer Methods in Applied Mechanics and Engineering
The Karhunen-Loève series expansion decomposes a Gaussian stochastic process
into an infinite series of pairwise uncorrelated random variables and pairwise
L2 orthogonal functions. The computational complexity of standard Galerkin finite
element formation and assembly techniques, as well as memory requirements of
direct solution techniques become quickly computationally intractable with
increasing polynomial degree and the number of elements. In this work we
present a novel matrix-free solution strategy that scales optimally with
the problem size, is indepedent of the polynomial degree and is emberassingly
parallel. A high-order three-dimensional benchmark
illustrates exceptional computational performance combined with high
accuracy and robustness.
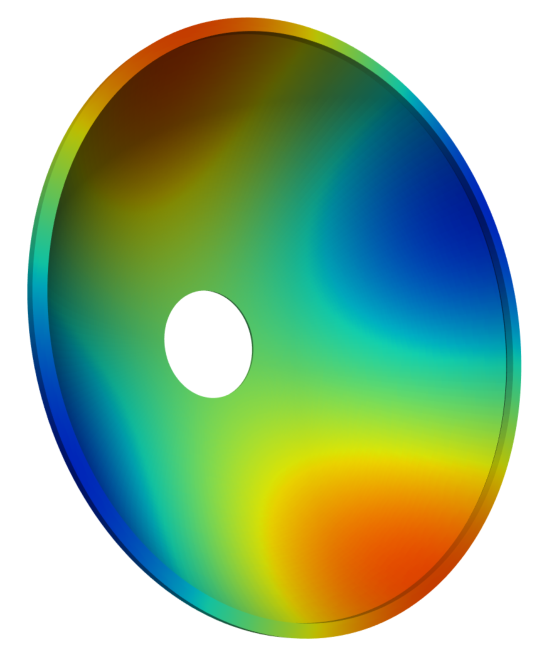
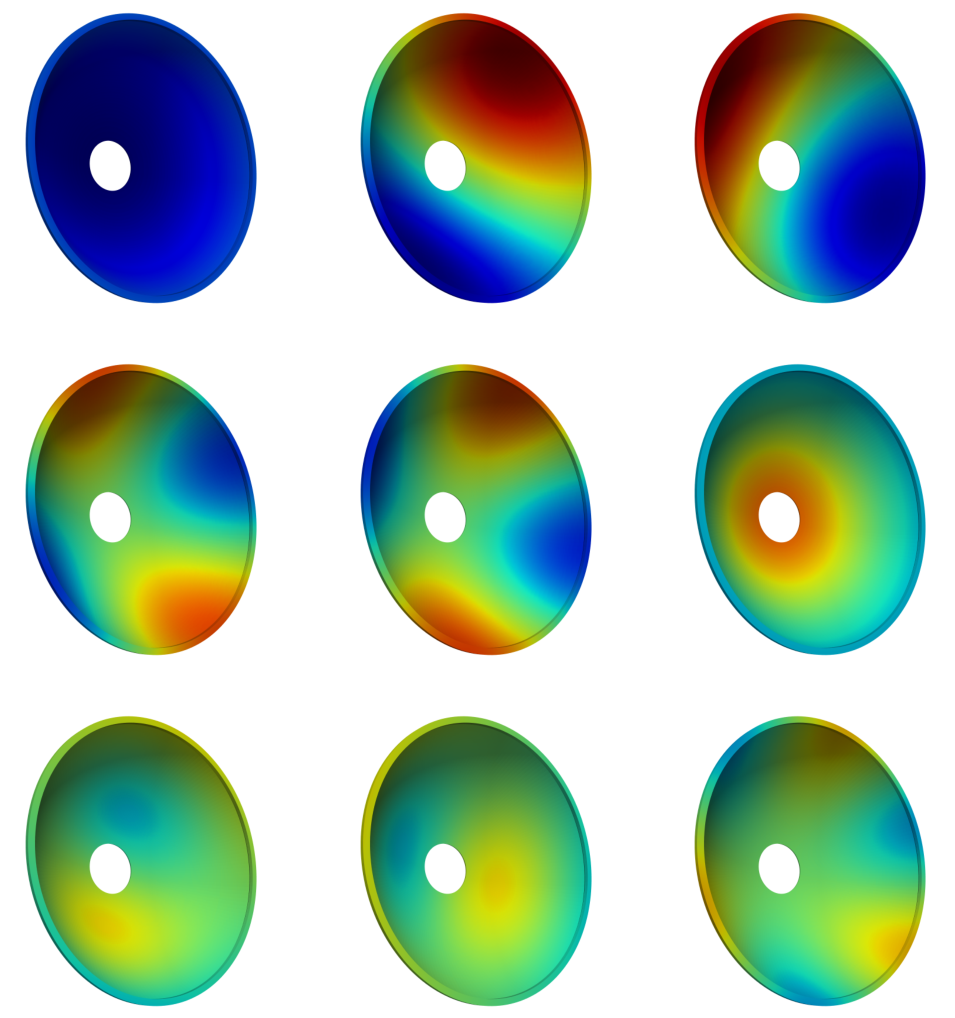
Electrostatic sensor modeling for torque measurements
M.L. Mika, M. Dannert, F. Mett, H. Weber, W. Mathis and U. Nackenhorst
September 21, 2017;
Advances in Radio Science
Based on a simple draft of an exemplary measurement setup,
this paper discusses the general idea behind an electrostatic
capacitive torque sensor. For better understanding of the working
principle of the sensor the electrostatics, the geometry and the mechanics of
the considered measurement setup are modeled. (undergraduate student project)
Visualization of finite element analysis results on 3D printed models
M.L. Mika, K. Dees and U. Nackenhorst
April 14, 2017;
This project explores the
possibilities of visualization of finite element analysis results using
3D printed models. By outer-surface extraction and implementation of a
VRML interface the interpolated datasets are prepared for a 3D print. (undergraduate student project)